If \(a\ge 0\) and \(b\ge 0\) and \(p>1\) and \(q>1\) such that
\[ \frac{1}{p}+\frac{1}{q}=1, \]then
\[ ab\le \frac{a^p}{p} + \frac{b^q}{q}. \]The equality holds if and only if \(a^b=b^q\).
Since \(p-1=\frac{1}{q-1}\), the graph \(y=x^{p-1}\) is also the graph \(x=y^{q-1}\). Since the area of the rectangle \(a,b\) cannot be larger than \(\int_{0}^a x^{p-1} \,dx\) and \(\int_{0}^b y^{q-1} \,dy\) (see figure below), we find by integration
\[ ab \le \frac{a^p}{p}+\frac{b^q}{q}. \]The equality holds if and only if \(a^b=b^q\).
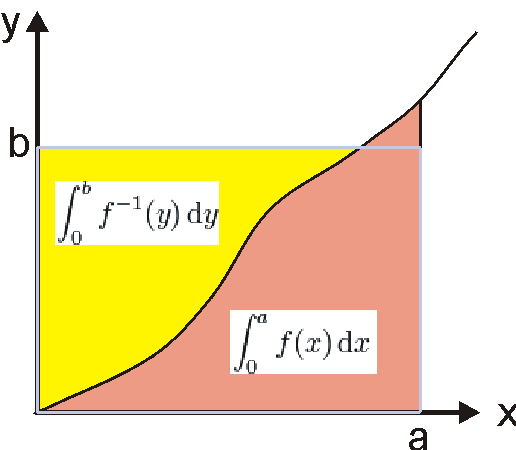
The area of the rectangle \(a,b\) cannot be larger that the sum of the area of the functions \(f\) (red) and \(f^{-1}\) (yellow).
For \(a=0\) and \(b=0\) the inequality is satisfied. Since the logarithm is concave, we find
\[ \log (\frac{1}{p}a^p + \frac{1}{q}b^q) \ge \frac{1}{p}\log (a^p) + \frac{1}{q}\log (a^q) = \log a + \log b = \log ab, \]where the inequality hold if and only if \(a^p=b^q\). By exponentiating we obtain Young’s inequality.
Let \(a,b\in \mathbb{R}\) and \(\varepsilon>0\). Then
- \(ab\le \frac{1}{2}(a^2+b^2)\) (Cauchy’s inequality )
- \(ab\le \frac{a^2}{2\varepsilon}+\frac{\varepsilon b^2}{2}\) (Peter-Paul inequality )